Is your thinking chaotic? There’s a model for that.
October 21, 2015
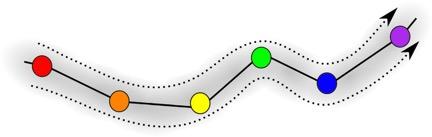
A representation of a stable sequential working memory; different information items or memory patterns are shown in different colors. (credit: Image adopted from Rabinovich, M.I. et al. (2014))
Try to remember a phone number. You’re now using “sequential memory,” in which your mind processes a sequence of numbers, events, or ideas. It underlies how people think, perceive, and interact as social beings. To understand how sequential memory works, researchers have built mathematical models that mimic this process.
Cognitive modes
Taking this a step further, Mikhail Rabinovich, a physicist and neurocognitive scientist at the University of California, San Diego, and a group of researchers have now mathematically modeled how the mind switches among different ways of thinking about a sequence of objects, events, or ideas that are based on the activity of “cognitive modes.”
The new model, described in an open-access paper in the journal Chaos, may help scientists understand a variety of human psychiatric conditions that may involve sequential memory, including obsessive-compulsive disorder, bipolar, and attention deficit disorder, schizophrenia and autism.
Cognitive modes are the basic states of neural activity. Thinking, perceiving, and any other neural activity involve various parts of the brain that work together in concert, taking on well-defined patterns.
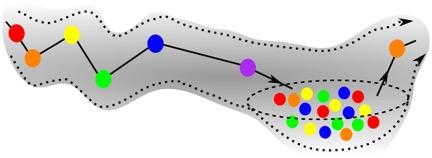
A pathological case (in particular, schizophrenia). The sequence is unstable — the initial sequence enters a chaotic valley after the purple unit. This happens when cognitive inhibition is weak. (credit: adopted from Rabinovich, M.I. et al. (2014))
Binding process
When the mind has sequential thoughts, the cognitive modes underlying neural activity switch among different modalities. This switching is called a binding process, because the mind “binds” each cognitive mode to a certain modality.

Limitless (credit: CBS)
Consider the TV show Limitless. In the show, FBI consultant Brian Finch, aided by the fictional cognitive enhancer NZT, is able to fluidly switch between complex sets of information (modalities), such as phone numbers, using different cognitive modes — rapidly processing a series of phone numbers of suspects on a screen, or analyzing a complex diagram showing potential criminal connections, then explaining it to colleagues, all without losing a beat.
In the new analysis, the mathematicians proved a theorem to show that in their model, this binding process is robust and able to withstand perturbations from the random disturbances in the brain. Your mind is full of other irregular neural signals — from things like other neural processes or external, sensory stimuli and distractions — but if they’re not too big, they don’t affect the thinking process.
This model could be used to better understand a variety of psychiatric disorders, such as obsessive-compulsive disorder, bipolar disorder, and attention deficit disorder, Rabinovich said. The way the mind binds to different modalities, and how such binding depends on time, may be related to conditions such as autism and schizophrenia. For example, some experiments suggest that for people with these conditions, the capacity of sequential binding memory is smaller.
Rabinovich worked with Valentin Afraimovich and Xue Gong, mathematicians at the Autonomous University of San Luis Potosi in Mexico and Ohio University, respectively.
Abstract of Sequential memory: Binding dynamics
Temporal order memories are critical for everyday animal and human functioning. Experiments and our own experience show that the binding or association of various features of an event together and the maintaining of multimodality events in sequential order are the key components of any sequential memories—episodic, semantic, working, etc. We study a robustness of binding sequential dynamics based on our previously introduced model in the form of generalized Lotka-Volterra equations. In the phase space of the model, there exists a multi-dimensional binding heteroclinic network consisting of saddle equilibrium points and heteroclinic trajectories joining them. We prove here the robustness of the binding sequential dynamics, i.e., the feasibility phenomenon for coupled heteroclinic networks: for each collection of successive heteroclinic trajectories inside the unified networks, there is an open set of initial points such that the trajectory going through each of them follows the prescribed collection staying in a small neighborhood of it. We show also that the symbolic complexity function of the system restricted to this neighborhood is a polynomial of degree L − 1, where L is the number of modalities.
