Simple mathematical pattern describes shape of neuron ‘jungle’
June 22, 2012
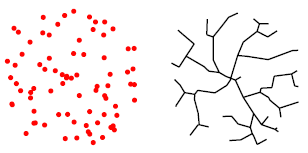
Neuron shape model: target points (red) distributed in a spherical volume and connected to optimize wiring in a tree (black) (credit: H. Cuntz et al./PNAS)
University College London (UCL) neuroscientists have found that there is a simple pattern that describes the tree-like shape of all neurons.
Neurons look remarkably like trees, and connect to other cells with many branches that effectively act like wires in an electrical circuit, carrying impulses that represent sensation, emotion, thought and action.
Over 100 years ago, Santiago Ramon y Cajal, the father of modern neuroscience, sought to systematically describe the shapes of neurons, and was convinced that there must be a unifying principle underlying their diversity.
Cajal proposed that neurons spread out their branches so as to use as little wiring as possible to reach other cells in the network. Reducing the amount of wiring between cells provides additional space to pack more neurons into the brain, and therefore increases its processing power.
New work by UCL neuroscientists has revisited this century-old hypothesis using modern computational methods. They show that a simple computer program that connects points with as little wiring as possible can produce tree-like shapes that are indistinguishable from real neurons — and also happen to be very beautiful.
They also show that the shape of neurons follows a simple mathematical relationship called a power law*: dendrites grow to fill a target space in an optimal manner and, similar to a minimum spanning tree, use the least amount of wiring to reach all synaptic contacts.
Power laws have been shown to be common across the natural world, and often point to simple rules underlying complex structures. Dr. Herman Cuntz (UCL Wolfson Institute for Biomedical Research) and colleagues find that the power law holds true for many types of neurons gathered from across the animal kingdom, providing strong evidence for Ramon y Cajal’s general principle.
The UCL team further tested the theory by examining neurons in the olfactory bulb, a part of the brain where new brain cells are constantly being formed. These neurons grow and form new connections even in the adult brain, and therefore provide a unique window into the rules behind the development of neural trees in a mature neural circuit.
The team analyzed the change in shape of the newborn olfactory neurons over several days, and found that the growth of these neurons also follows the power law, providing further evidence to support the theory.
“The ultimate goal of neuroscience is to understand how the impenetrable neural jungle can give rise to the complexity of behavior,” Cuntz said. “Our findings confirm Cajal’s original far-reaching insight that there is a simple pattern behind the circuitry, and provide hope that neuroscientists will someday be able to see the forest for the trees.”
*A 2/3 power law: L = (3/4π)1/3 × V1/3n2/3 where n is the number of dendritic sections to make up the tree, L is the total length of these sections, and V is the total volume
