Thinking quantitatively about technological progress
July 11, 2011
I have been thinking about progress a bit recently, mainly because I would like to develop a mathematical model of how brain scanning technology and computational neuroscience might develop.
Experience curves
In general, I think the most solid evidence of technological progress is Wrightean experience curves. These are well documented in economics and found everywhere: typically the cost (or time) of manufacturing per unit behaves as x^a, where a<0 (typically something like -0.1) and x is the number of units produced so far. When you make more things, you learn how to make the process better.

Experience curve (credit: Bruce Henderson, Boston Consulting Group)
Performance curves
On the output side, we have performance curves: how many units of something useful can we get per dollar. The Santa Fe Institute performance curve database is full of interesting evidence of things getting better/cheaper. Bela Nagy has argued that typically we see “Sahal’s Law“: exponentially increasing sales (since a tech becomes cheaper and more ubiquitous), together with exponential progress, produces Wright’s experience curves.
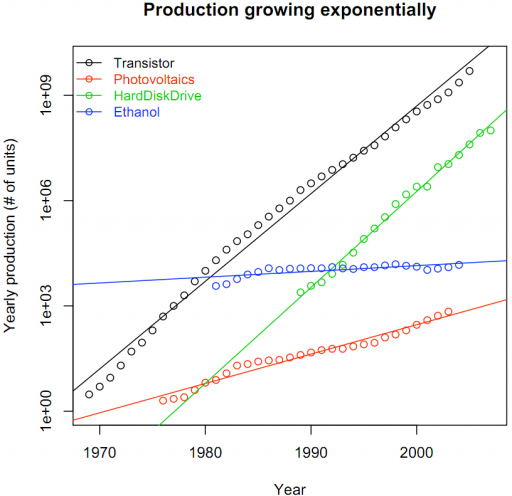
Production growing exponentially (credit: Béla Nagy, Santa Fe Institute)
One interesting problem might be that some techs are limited because of the number of units sold will eventually level off. In sales of new technology we see Bass curves: a sigmoid curve where at first a handful of early adopters get it, then more and more get it (since people copy each other this is roughly exponential) and then a leveling off as most potential buyers already got it.

Bass diffusion model of new adopters (credit: Frank M. Bass, University of Texas at Dallas)
Lots of literature on it, useless for forecasting (due to noise sensitivity in the early days). If Bela is right, this would mean that a technology obeying the Moore-Sahal-Wright relations would certainly follow a straight line in the “total units sold” vs. “cost per unit” diagram, but there would be a limit point since the total units sold eventually levels off (once you have railroads to every city, building another one will not be useful; once everybody has good enough graphics cards they will buy much fewer).
The technology stagnates, and this is not because of any fundamental physics or engineering limit. The real limit is lack of economic incentives for becoming much better.
Discontinuities
Another aspect that I find really interesting is whether a field has sudden jumps or continuous growth. Consider how many fluid dynamics calculations you can get per dollar. You have an underlying Moore’s law exponential, but discrete algorithmic improvements create big jumps as more efficient ways of calculating are discovered.
Typically, these improvements are big, a decade of Moore or so. But this mainly happens in some fields like software (chess program performance behaves like this, and I suspect — if we ever could get a good performance measure — AI does too), where a bright idea changes the process a lot. It is much more rare in fields constrained by physics (mining?) or where the tech is composed of a myriad interacting components (cars?).
Any other approaches you know of in thinking quantitatively about technological progress?
